Density functional theory
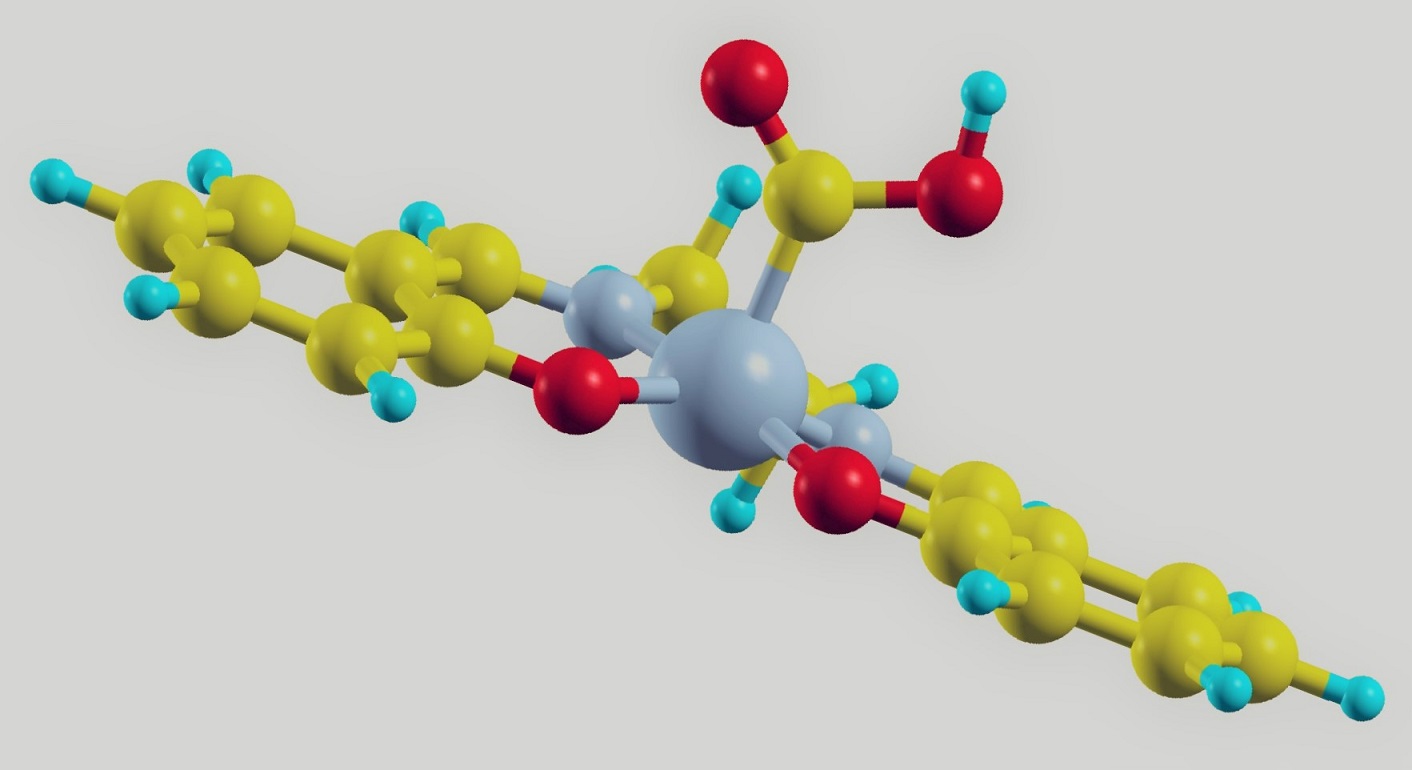SanD researchers employ first-principles density functional theory (DFT) to investigate various 2D and bulk materials. DFT is a very efficient method to calculate the electronic properties of a material as it simplifies the many-body problem to non-interacting one-electron Schrödinger-like equations and expresses the energies as a functional of the density. Using DFT, various physical properties are investigated including electronic, magnetic, topological, and thickness-dependent properties.
Statistical Field Theory
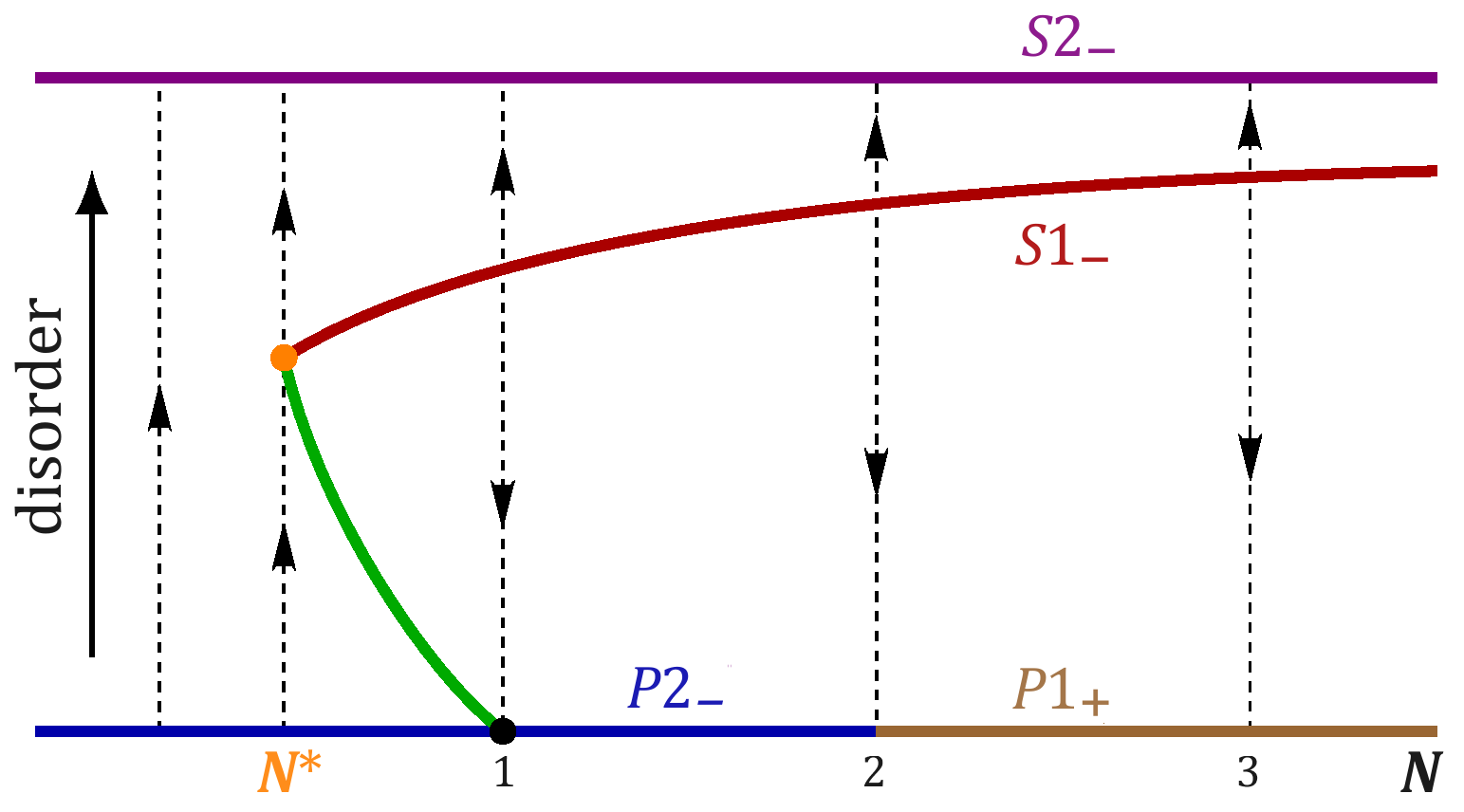At criticality, the correlation length of a statistical model diverges and the system loses a characteristic length scale. This scale invariance at the critical point makes it natural to model a wide range of systems, classical or quantum, in terms of statistical field theory. This allows the use of field theoretical methods with the understanding that critical points correspond to renormalization group fixed points of a given model in theory space. This picture sheds light into the emerging universal properties at critical points in systems undergoing phase transitions.
Spin transport and spin-orbit interactions
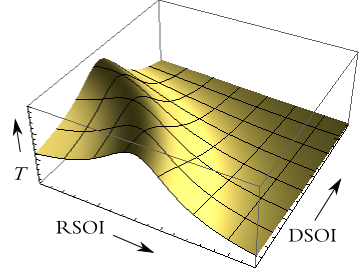SanD researchers study the effects of Rashba and Dresselhaus spin-orbit interactions (SOI) on spin transport in quasione-dimensional electron systems. Calculating the transport coefficients of the different spin components allows us to determine the degree of polarization of the spin current. The results of this study may be used to find out how spin-orbit interactions can be used to engineer spintronics devices.
Entanglement and quantum computing
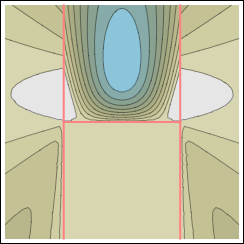Entanglement is a robust quantifier of quantum correlations in many-body systems. We do analytical studies of entanglement in spin chains, low-dimensional gases, and Gaussian states. In many cases of interest, subsystems of pure states at zero temperature display quantum fluctuations with the same statistical properties as in effective thermal models.
SanD also performs numerical simulations of quantum algorithms like Grover's algorithm in order to gain a deeper understanding of how experimental conditions can affect implementations of quantum computing.
Two-dimensional electron systems
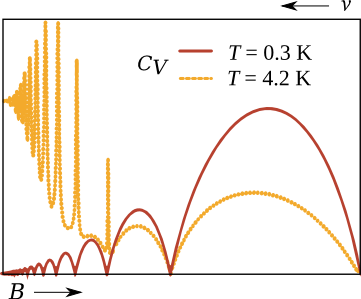
The study of two-dimensional electron systems (2DES) is essential to understanding the quantum Hall effect. SanD numerically and analytically investigates the behavior of the temperature- and magnetic field-dependent energy fluctuations in the 2DES spectra and its corresponding density of states. It is found that Landau level broadening due to disorder in a 2DES causes variations in its interlevel and intralevel excitations. At a characteristic low temperature, this broadening parameter has no effect on the specific heat of the system.
Parallel and high-performance computing
SanD is developing a custom-built heterogeneous Linux cluster for its computational tasks. Our high-performance computing (HPC) facility currently consists of 84 computing cores and 7296 CUDA cores. In addition to learning how to use open-source production code like LAMMPS (molecular dynamics) and Quantum ESPRESSO (density functional theory) our students also acquire HPC systems administration skills and expertise.